Алгоритми: будуємо дерева за правилами

Інформатика без комп’ютера

Алгоритм — одне з основних понять інформатики. Ми звикли його вивчати напередодні навчання програмуванню. Але ж ми навіть і не помічаємо наскільки багато у повсякденному житті ми використовуємо алгоритми — рецепт виготовлення страв, інструкція по роботі з електроприладом тощо. Та й у дитячому садку можна ознайомлювати дітей з алгоритмами (звичайно термін ми не називаємо, але навчаємо діяти за алгоритмами та записувати їх). Але ж з алгоритмами можна познайомити дітей у звичному для них середовищі і працювати із вже давно знайомими геометричними фігурами. Почнімо!

Згадаємо у яких завданнях ми використовували геометричні фігури. Що ми з них будували? Спочатку з геометричних фігур ми будували яскраві візерунки, композиції силуетів тварин, людей, машин, рослин тощо; потім — геометричні фігури більшого розміру; малювали карти руху геометричних фігур доріжками міста. Сьогодні я розповім як будувати з геометричних фігур дерева за правилами. Тільки листочки у цих дерев незвичайні — їх утворюють різнобарвні геометричні фігури.

Ці задачі можна розв’язувати і з молодшими школярами: сподіваюсь, що таке ознайомлення з алгоритмами не буде складним ані малятам, ані вчителям.

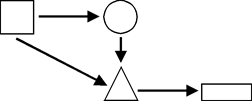
Правила для побудови дерев записуються у вигляді направлених графів. Кожне дерево будується за своїм правилом. Завдання на побудову дерев мають тільки один розв’язок: за кожним правилом можна побудувати тільки одне дерево.

Ці завдання у технології «Логіки світу» пропонуються для старших дошкільників та першокласників. Дерева з геометричних фігур можна малювати на папері або будувати з геометричних фігур з набору (див. попередні статті), з’єднуючи їх паличками для рахування.

У правилах побудови дерев не визначений колір геометричних фігур, тому немає жодних обмежень зафарбування геометричних фігур на гілочках. Кожна дитина може зафарбувати геометричні фігури на гілочках так, як їй заманеться.

Завдання на побудову дерев за правилами (алгоритмами) є ще одним прикладом завдань з використанням алгоритмів. Розв’язуючи їх, діти вивчають такі основні властивості алгоритмів:

• однозначність (кожний крок алгоритму має бути чітко визначеним; кожна людина, виконуючи алгоритм, однаково виконуватиме усі кроки алгоритму) — всі люди, які користуються одним і тим самим правилом, завжди побудують дерева з однаковими гілочками;

• дискретність (алгоритм складається із кроків, які виконуються у чітко визначеній послідовності) — ми будуємо гілочки на дереві поступово, кожна стрілочка в правилі — це крок до побудови всього дерева, напрямок стрілочок визначає послідовність кроків побудови дерева;

• результативність (виконання алгоритму завжди має приводити до результату) — якщо правило написано правильно, ми завжди побудуємо за ним дерево;

• кінцевість (результат виконання алгоритму досягається через кінцеву кількість кроків) — якщо правило написано правильно, ми побудуємо дерево, зробивши обмежену кількість кроків.

У цих завданнях використовується графічний спосіб задання алгоритмів. Кожна стрілочка в правилі побудови дерева — це окремий крок алгоритму.

Розглянемо деякі завдання цього типу.

Задача 1

Побудуй дерево за правилом.

Усі гілочки дерева починаються з однієї геометричної фігури. Насамперед нам потрібно її знайти: у правилі побудови дерева всі стрілочки йдуть від цієї геометричної фігури до інших геометричних фігур, а не навпаки. Знайдем таку геометричну фігуру в правилі. У цьому правилі усі гілочки починатимуться з квадрата. Виділимо його, зафарбувавши іншим кольором (наприклад, червоним).

Тепер можна починати будувати дерево. Біля стовбура намалюємо квадрат і почнемо будувати першу гілочку. Якою буде наступна геометрична фігура на цій гілочці? Стежимо за стрілочками у правилі: одна з стрілочок біля квадрата вказує на круг. Таким чином, круг буде другою геометричною фігурою на цій гілочці.

Далі стежимо за стрілочками в правилі і будуємо першу гілочку дерева. Де ж закінчується ця гілочка? Від прямокутника до інших геометричних фігур не спрямована жодна стрілочка в правилі, тому на ньому закінчується перша гілочка.

Щоб діти краще орієнтувалися під час пошуку фігур для гілочок на дереві, можна стрілочки, які відповідають в правилі знайденій гілочці, обводити кольоровим олівцем. Малюк вибере для кожної гілочки дерева свій колір. Таким самим кольором можна зафарбовувати геометричні фігури — вийде дерево, в якого кожна гілочка матиме свій колір. Таким чином, малюнок стане більш наочним.

Побудуємо другу гілочку дерева. Від квадрата друга стрілочка в правилі йде до трикутника. Тому другою геометричною фігурою на цій гілочці буде трикутник. Від трикутника стрілочка йде до прямокутника. Прямокутник — остання геометрична фігура на гілочці.

Ми пройшли всіма можливими шляхами за стрілочками у правилі. Зараз ми не можемо побудувати жодної гілочки на дереві, яка б відрізнялася від уже побудованих гілочок. Результатом рішення задачі є дерево, зображене на малюнку нижче.

При побудові дерев за правилами майбутні школярики вивчають таке поняття, як «цикл» (підкреслю, поняття «цикл» у технології «Логіки світу» не вводиться, діти вивчають його несвідомо, на інтуїтивному рівні); вчаться знаходити цикли в написаних правилах; виправляють помилки, спричинені неправильним використанням циклів.

У завданнях на побудову дерев за правилами наслідком використання циклів є порушення властивості «кінцевість» алгоритму. Ми ніяк не можемо закінчити будувати гілочку дерева: вона не має ані початку, ані кінця.

У наступній публікації ми розглянемо задачі, де в правилі використовується цикл.

Ірина СТЕЦЕНКО,

науковий співробітник Міжнародного науково-навчального центру інформаційних технологій та систем Національної академії наук України

та Міністерства освіти і науки України,

автор технології «Логіки світу»

для дітей від 4 до 12 років

Дізнайтеся про що блог

Читайте роздуми щодо теми блогу

Автор: Ірина Стеценко