Сходинки маленького дослідника: конструювання з геометричних фігур
Початок статті про дослідження читайте за посиланням
 Суттєвою особливістю занять з інтелектуального розвитку на відміну від традиційних предметних уроків є перенесення акценту з результату на процес розв’язування і його обгрунтування.
Суттєвою особливістю занять з інтелектуального розвитку на відміну від традиційних предметних уроків є перенесення акценту з результату на процес розв’язування і його обгрунтування.
У результаті проведення таких занять діти здобувають також необхідні інтелектуальні вміння, які використовують на інших заняттях, що приводить до перших успіхів дітей, у них виникає інтерес до навчання.
Розвиток
мислення дітей тісно пов’язано з формуванням прийомів мислення у процесі їхньої
навчальної діяльності. Ці прийоми мислення (аналіз, синтез, узагальнення,
абстагування тощо) виступають також, як специфічні методи наукового
дослідження, які особливо яскраво проявляються під час розв’язування задач.
У
цілеспрямованому розвитку мислення дітей задачі є найприроднішим і
найефективнішим засобом. Мислення
психологічно виступає як діяльність розв’язування задач. Доктор
психологічних наук, професор А. В. Брушлинський підкреслює, що розвиток
мислення відбувається саме під час розв’язування задач, коли перед людиною
постають проблеми і запитання, які їй по силам, вона самостійно формулює їх, а
потім вирішує.
Отже, розвиток
мислення і творчих здібностей відбувається під час роздумів дітей над задачами.
Задачею може бути будь-яке завдання, що вимагає здійснення будь-якого
пізнавального акту, будь-який навчальний текст, що потрібно засвоїти. До
розвивальних задач відносять:
- задачі, для рішення яких не потрібні нові знання по предмету, але потрібно використати знання в іншій комбінації;
- задачі, за допомогою яких і на основі яких здобуваються і поглиблюються знання по предмету.
Задачі
із розвивальними функціями не повинні бути об’єктом вивчення, вони призначені
для розвитку мислення. Найбільшу
користь розвивальні задачі приносять тоді, коли їх розв’язують без попередньої
підготовки, вони достатньо різноманітні за змістом і способом розв’язування. Рішення
задач із розвивальними функціями ніколи не доводиться до навичок. Діти —
кожний в міру своїх можливостей — просто розв’язують ці задачі.
Технологію «Логіки світу» спрямовано на розвиток мислення дітей. Розв’язуючи
задачі технології, діти вчаться грамотно
обгрунтовувати свою точку зору, самостійно приймати рішення, не боятися задач з
багатьма варіантами розв’язку.
У перших
дослідженнях задачу формулює педагог (принаймні, у загальному вигляді): дітям
ще важко самостійно точно її сформулювати. Потім за допомогою вчителя або
самостійно діти детальніше розглядають задачу і повністю формулюють її.
Розглянемо задачі технології «Логіки
світу», під час розв’язування яких діти можуть учитися досліджувати. Слід підкреслити, що дослідженням може стати майже кожна задача
технології «Логіки світу», а також багато задач, які ви розв’язуєте з дітьми на
заняттях. Головне — цікаво побудувати заняття таким чином, щоб показати дітям сенс дослідницької
діяльності.
Далі пропоную задачі,
кожна з яких може стати окремим дослідженням.
Задача 1 (для дітей 4–5
років)
Уважно роздивись цей малюнок. Із яких геометричних фігур він складається?
Приготуй набір геометричних фігур для
конструювання.
Розкажи, які геометричні фігури з набору
треба приготувати для викладення курчатка, ялинок, сонечка, хатинки. Якого
кольору ці фігури? Вибери з набору потрібні для викладення композиції
геометричні фігури.
Виклади композицію. Заверши її так, як
тобі подобається.
Умова задачі сформульована
у зошиті. Але слід розібратися докладніше у вихідних даних. Який
набір для конструювання можна використовувати? Такий набір є у кожного на
столі. Запропонуйте дітям уважно роздивитися геометричні фігури, які входять в
набір, визначити, які з них необхідно використати для викладення композиції.
В технології «Логіки світу» використовується набір з найпростіших
геометричних фігур зеленого, червоного і жовтого кольорів (по 5 геометричних
фігур кожного кольору).
Одразу всі
силуети викладати складно, тому задачу викладання композиції
вирішуватимемо поетапно. Визначимо послідовність викладання окремих
силуетів, тобто сформулюємо проміжні результати.
У малюків ще
немає досвіду конструювання силуетів, тому їм не зрозуміло з якого силуету слід
починати викладання композиції. Можливо, спочатку викладатимемо силует, який
сподобався найбільше? Можливо, краще починати з силуету, який викладати найлегше? (Але це не єдині критерії визначення послідовності викладання композицій, можливо діти запропонують свій критерій і він теж буде
правильним.)
Малюки пильно
придивляються до намальованої композиції і визначають послідовність її викладання. Одразу здається, що хатинку викласти найлегше: вона складається лише
з двох геометричних фігур — квадрата і трикутника. Отже пропоную таку
послідовність викладання композиції.
Звичайно,
послідовність конструювання лише обговорюється разом з дітьми, схему я навела
для наочності.
Настав час висування гіпотез.
Відзначу, тільки педагог знає, що на зразку всі силуети повністю поділені на
геометричні фігури з набору. Діти кожний силует можуть поділити на геометричні
фігури інакше, ніж намальовано, хоч таке трапляється й не досить часто,
принаймні у чотирирічних дітей.
Нижче я навела
різні варіанти викладання хатинки. Малюки визначають гіпотезу викладання силуету (з яких саме геометричних фігур можна викласти силует) і
одразу викладають його (перевіряють гіпотезу). Щоб дітям
було легше аналізувати отримані результати, доцільно поруч викладати кілька хатинок. Потім поруч з ними діти викладатимуть інші силуети.
В процесі
конструювання наступних силуетів діти знаходитимуть неправильні гіпотези
(неправильно викладені силуети) і залишатимуть правильно викладені силуети. Потім
залишаться тільки правильні гіпотези і малюки складуть композицію повністю.
Під час викладання композицій в багатьох випадках важко одразу визначити наскільки правильно викладено силует: треба зачекати викладення інших силуетів композиції. Але
уважно порівнявши зразок і викладені хатинки, можна визначитись щодо
правильності деяких гіпотез.
У нашому
випадку одразу видно, що п’ята і шоста гіпотези неправильні. У хатинки, викладеної за п’ятою гіпотезою, надто маленький дах, а у хатинки, викладеної за шостою гіпотезою, форма даху не така, як на зразку. Часто діти
помічають, що хатинка, викладена за першою гіпотезою, надто маленька. Але її ще немає з
чим порівнювати (ще не побудовано наступні силуети), тому цю помилку не всі
малюки знаходять одразу.
Відзначу
також, що друга і третя гіпотези майже однакові (під час конструювання увага
переважно звертається на контури силуетів): віконечко прикрашає силует будинка,
але не є обов’язковим його елементом. Тому діти серед цих силуетів можуть
обирати той, який їм подобається найбільше. Скласти враження щодо правильності
інших гіпотез важко, отож час перейти до викладення другого
силуету.
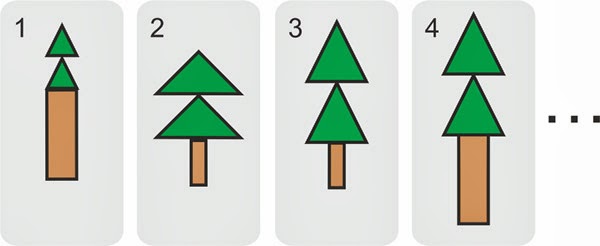
Одразу
помітно, що у ялинок, викладених за першою і четвертою гіпотезами, порушено пропорції:
стовбури надто великі. Ці гіпотези неправильні. Ялинка, викладена за другою
гіпотезою, виглядає не зовсім так, як на зразку. Але не всі маленькі діти це
помічають (особливо важко це помітити, якщо третю гіпотезу не відсунуто): у них
не вистачає досвіду конструювання. Ця ялинка схожа на зразок, тому другу гіпотезу,
особливо для чотирирічних малюків, я не вважаю грубою помилкою.
Тепер настав
час зосередити увагу на порівнянні викладених ялинок і хатинок. Тут вже
одразу помітно, що хатинка, яка викладена за першою гіпотезою, маленька.
Нарешті ми викладаємо курчатко. Спочатку здається, що курчатко викладається з маленьких
кіл. Але, поклавши їх в композицію, діти одразу бачать: курчатко вийде
замаленьким, слід використати більші кола. Так малюки навчаються корегувати
поведінку в залежності від результатів експерименту. Вони висувають наступні
гіпотези.
Щось лапки у курчатка, викладеного за другою гіпотезою, вийшли дуже
великими. Діти уважно дивляться на зразок: лапки намальовані значно меншими
порівняно з кругами, і курчатко виглядає симпатичніше. Виберемо з набору
маленькі червоні трикутники: вони більше підходять для викладення лапок
курчатка. Тепер викладене курчатко більше схоже на силует на зразку. (Надалі
діти вже знатимуть, як добирати величину геометричних фігур. Трохи згодом вони
за пропорціями силуетів і на основі власного досвіду правильно визначатимуть
величину геометричних фігур, з яких складається силует.)
Отже, композиція майже викладена. Діти вбирають один з будинків. Усі вони
однакової величини, складаються майже з однакових геометричних фігур (до складу
кожного будинку входить великий квадрат і великий трикутник, тільки в одному
будинку великий трикутник складається з чотирьох маленьких: будинок вийшов
різнокольоровим). Тож який будинок вибрати? Враховуючи все згадане вище,
будинки відрізняються лише дизайном: малюки можуть вибрати той, що їм
подобається найбільше. Композиція завершена, дослідження закінчено.
Відзначу тільки, що етап аналізу результатів майже повністю проводився
одразу після отримання кожного проміжного результату, в цьому завданні так
робити найдоцільніше.
Як ми щойно
побачили, і у завданнях на конструювання іноді можна знайти кілька варіантів
рішення. Запропонуйте дітям де це можливо знайти різні варіанти рішення і
проаналізувати їх. Які розв’язки схожі, а які відрізняються? Чим
відрізняються розв’язки? Яке завдання має лише одне рішення? Спробуйте
пояснити, чому це завдання має тільки одне рішення.
У наступних статтях блогу читайте про приклади розв’язування задач за допомогою дослідження.
науковий співробітник Міжнародного науково-навчального
центру інформаційних технологій та систем Національної академії наук України
та Міністерства освіти і науки України,
автор технології «Логіки світу»
для дітей від 4 до 12 років