Подорож стежинками з правилами з використанням форми та логічних операцій

Нині поняття алгоритм часто пов’язують тільки з інформатикою, але в алгоритмах часто використовуються операції алгебри логіки та й складно зараз уявити багато наук без використання алгоритмів. У попередній публікації я розповідала про правила з використанням кольорів та логічних операції «ні», «і». Сьогодні розповім як можна ускладнювати правила, ввівши форму геометричних фігур.
На
малюнку нижче зображені приклади правил руху, в яких використовується тільки
одна геометрична фігура.
|
|
ця доріжка веде до
хатинок, де живуть тільки прямокутники;
|
|
|
ця доріжка веде до
хатинок, де живуть всі не трикутники.
|
У
найскладніших правилах руху використовуються одразу кілька геометричних фігур
різних типів.
|
|
ця доріжка веде до
хатинки, де не живуть всі квадрати і всі трикутники;
|
ця доріжка веде до
хатинки, де живуть тільки круги і прямокутники;
|
|
ця доріжка веде до
хатинки, де не живуть всі трикутники, всі круги і всі прямокутники.
|
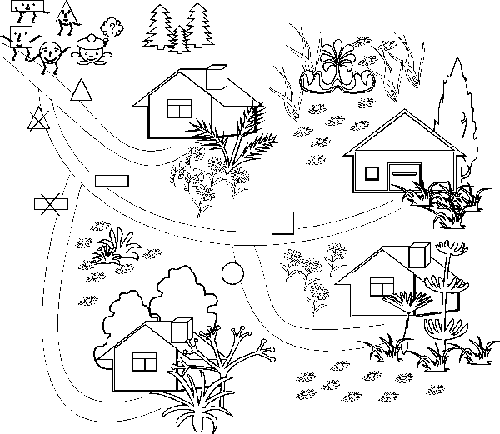
Задача 1
Допоможи геометричним фігурам знайти
свої хатинки, користуючись правилами руху фігур доріжками міста.
На
цій карті міста доріжок більше, ніж у попередніх задачах. Щоб геометричні
фігури довго не блукали, розшукуючи свої домівки, правила намальовано на
доріжках, а не біля хатинок. Кожна геометрична фігура знає веде доріжка до її
хатинки чи ні.
Уявимо
як рухаються геометричні фігури доріжками з правилами.
Які
геометричні фігури можуть йти до своєї хатинки доріжкою з правилом?
«По
цій доріжці можуть йти тільки прямокутники.» Який колір повинні мати
прямокутники, які йдуть по цій доріжці? Чи можуть йти по доріжці синій
прямокутник, жовтий прямокутник, зелений квадрат, червоний прямокутник, коло?
(Ці запитання допомагають дітям краще зрозуміти, що в правилах цього типу увага
привертається тільки до типу геометричних фігур, а не до їх кольору. Саме це
відрізняє ці правила від правил у
попередніх задачах.)
Які
геометричні фігури підуть шукати свої хатинки далі? «Далі підуть круг,
трикутник і квадрат, тобто всі не прямокутники (на це вказує
правило).»
Користуючись
іншими правилами на карті, і ці геометричні фігури знайдуть своє житло. Кожна
геометрична фігура потрапить у певний будинок, жодна з них не залишиться без
житла і не заблукає, жодна геометрична фігура не може жити одразу ж у кількох
будинках.
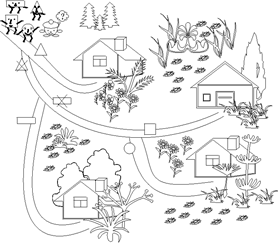
Задача 2
Допоможи геометричним фігурам знайти
свої хатинки, користуючись правилами руху фігур доріжками міста.
Поміркуй, чому в місті є порожні
хатинки. Чи є геометричні фігури, які не знайшли собі хатинок?
Спробуй змінити карту міста так, щоб
кожна геометрична фігура мала свою власну хатинку.
Спробуємо
знайти хатинку для кожної геометричної фігури. Фігури дійшли до першого
розгалудження доріг. Куди вони підуть далі? «Трикутник піде доріжкою до власної
хатинки. Ця доріжка позначена правилом.
Другою
доріжкою підуть всі інші геометричні фігури.» Фігури йдуть далі містом. Нарешті
з’являється друге розгалудження доріг. Куди яка геометрична фігура піде? «Всі
прямокутники підуть доріжкою з правилом.
Квадрат
і
круг підуть іншою доріжкою і знайдуть будинок, у якому і будуть жити.
Прямокутник піде далі шукати собі хатинку.» Нарешті він дійшов до останнього
розгалудження доріг. Куди він може йти? «Він не може нікуди йти далі, тому що
першою доріжкою можуть йти тільки квадрати, а другою — тільки круги. Але вони
пішли вже іншою доріжкою і житимуть в іншому будинку. Виявилось, що прямокутник
залишився без будинка, і в місті є аж два порожніх будинка.»
Спробуємо
виправити помилку на карті. Існує багато способів. Наведу деякі з них.
Можна
трикутник, круг і квадрат залишити жити в тих самих хатинках, змінивши правила
так, щоб прямокутник міг жити в одній із порожніх хатинок. «Можна поставити на
доріжку правило:
Тоді
прямокутник зможе йти доріжкою з цим правилом і знайде собі хатинку.»
Але
це надто просто! Як ще можна виправити помилку? Яке інше правило дає можливість
прямокутнику пройти одною з доріжок? «Наприклад, можна змінити правила так:
Прямокутник
не
квадрат і може йти цією доріжкою до будинка. Але у цих двох випадках одна з
хатинок залишиться порожньою.»
Спробуйте
виправити правила так, щоб всі геометричні фігури знайшли собі хатинки і у
місті не було порожніх хатинок. «Ми розмістимо геометричні фігури так:
прямокутник оселиться у хатинці після другого розгалудження доріг (в ньому за
попередніми варіантами рішення жили квадрат і круг), а круг і квадрат підуть
далі і оселяться у двох інших хатинках. У нас вийшла така карта міста.»
Розв’язуючи
будь-які задачі цього типу, в яких потрібно змінити карту міста, нагадайте дітям про перевірку зміненої
карти. Чи правильно змінили карту міста відповідно до умови завдання? Також
завжди потрібно перевіряти однозначність
правил руху геометричних фігур на карті міста: кожна фігура повинна мати тільки одну хатинку.
Дітям
завжди цікаво перевіряти не тільки своє рішення, а й дії іншої дитини. Нехай
діти поміняються зошитами, тоді кожна дитина буде перевірятиме рішення свого
товариша. Потім можна порівняти результат товариша із власним, спробувати разом
знайти і виправити помилки (якщо вони є). Так діти привчаються працювати не
тільки самостійно, а й у колективі, рахуватися з думками своїх товаришей. Які
правила руху геометричних фігур використав товариш? Чому він так зробив? А
може, тепер разом можна вигадати ще один варіант розв’язку цієї задачі? Діти
наочно бачать, що кожна задача має кілька різних варіантів розв’язку.
Задача 3
Допоможи геометричним фігурам знайти
свої хатинки, користуючись правилами руху фігур доріжками міста.
У цій
задачі правила ускладнюються. Поміркуй! Як можна прочитати правило з двома
геометричними фігурами? «Цією доріжкою не можуть йти всі квадрати і всі
трикутники.» Чи може йти цією доріжкою круг? «Круг може йти до свого будинка
цією доріжкою, тому що він не трикутник і не квадрат.» Які ще
геометричні фігури можуть йти цією доріжкою? «Цією доріжкою можуть йти всі
овали, прямокутники, п’ятикутники, шестикутники.» Намалюй, які чотирикутники
можуть йти цією доріжкою. «Цією доріжкою можуть йти такі чотирикутники:»
Діти
вже зрозуміли зміст правил, і їм неважко знайти будинки для геометричних фігур.
Задача 4
Допоможи геометричним фігурам знайти
свої хатинки, користуючись правилами руху фігур доріжками міста.
Поміркуй, чому геометричні фігури
заплуталися.
Спробуй виправити помилку в карті міста.
Пам’ятай: кожна фігура мусить знайти собі хатинку.
Давайте
розберемося, яка геометрична фігура у якій хатинці живе за картою міста.
Неважко визначитись які доріжки приведуть трикутник, круг і квадрат до своїх
будинків. Важче розібратися які геометричні фігури знайдуть свій будинок,
користуючись доріжкою з правилом:
Спочатку
«прочитаємо» правило: цією доріжкою до своєї хатинки не можуть йти квадрати і
круги, інші геометричні фігури можуть йти цією доріжкою до свого будинка. Які
геометричні фігури в нашій задачі можуть жити в будинку, до якого веде доріжка
з цим правилом? «Звичайно, це має бути прямокутник і трикутник.» Виходить,
що трикутник може жити одразу у двох будинках казкового міста. Він заплутався.
В якому будинку він живе? Якою доріжкою він має йти до власного будинка?
Виявляється карту міста побудовано неправильно. Треба виправити допущенну
помилку!
Здається
треба змінити правило на першій доріжці:
Але
тоді цією доріжкою зможуть йти до власного будинка і прямокутники, і квадрати,
і круги. Геометричні фігури заплутаються ще більше. Тільки трикутник буде точно
знати доріжку до свого будинка. Цей варіант не годиться!
Мабуть,
спробуємо виправити правила так:
Що в
нас вийшло? «Цією доріжкою може йти тільки прямокутник, тому що доріжкою
не
можуть йти всі квадрати, круги і трикутники. Для них у місті вже
знайшлися будинки.» Тепер карту міста побудовано правильно (нагадаю, що це
завдання, як і інші, має не один варіант рішення).
Задача 5
Геометричні фігури сидять у своїх
хатинках і не можуть вийти до лісу погуляти: у них загубилася карта міста, а
без неї вони ризикують заблукати. Допоможи фігурам скласти правильну карту
міста.
Це
перша задача, в якій діти не користуються вже готовою картою міста, а складають
її самі. Під час розгляду результатів рішення таких задач треба звертати увагу
на складність правил, що використані на побудованій карті міста, і вимагати вживання
правил з використанням «І» та «НЕ».
Розв’язуючи
такі задачі, зверніть увагу дітей на те, що існує дуже багато варіантів
розв’язку (деякі з варіантів наведені на малюнку нижче). Діти мають змогу
використовувати будь-які правила руху, вигадувати власні правила руху
геометричних фігур. Проаналізуйте разом із малюками кілька варіантів рішення.
Скільки різних варіантів придумали діти?
Перед
рішенням задачі варто пригадати, яка карта міста правильна, а яка ні. За правильною картою міста:
• кожна
геометрична фігура має хатинку;
• геометричні
фігури не блукають містом: вони точно знають якою доріжкою йти, і можуть жити
тільки в одній хатинці міста;
• у
місті не повинно бути порожніх хатинок (геометричні фігури живуть у кожній
хатинці міста).
Як переконатись,
що це завдання розв’язано правильно? Звичайно, спробувати самому знайти хатинку
для геометричної фігури, використавши вирізані геометричні фігури. А тепер
наведу приклади рішення цього завдання.
науковий співробітник Міжнародного науково-навчального центру інформаційних
технологій та систем Національної академії наук України
та Міністерства освіти і науки України,
автор технології «Логіки світу»
для дітей від 4 до 12 років