Смачна математика
Попередня публікація за посиланням — Частина 2 «Порівнюємо дроби»
Додаємо дроби — складаємо частинки
Щоб
зрозуміти як слід додавати дроби, пригадайте з дітьми зміст арифметичної операції
додавання. Ви давно вже так дієте з натуральними числами, а отже додаєте
обʼєкти.
Щоб
додати частини одну до одної потрібно їх скласти (покласти одну біля одної, або
висипати в одну ємність, або …) разом. Тож спробуємо скласти ціле з різних
частинок і розповісти що саме отримали в результаті за допомогою дроби. Раніше,
коли ми складали обʼєкти, то зазначали 3 лялечки + 4 лялечки = 7 лялечок або ж
2 машинки + 4 машинки = 6 машинок. А тепер рахуємо частини цілого.
Як
це виглядає? Беремо частинки, які відповідають першому дробу, складаємо з них
частину цілого, потім беремо частинки, які відповідають другому дробу, і додаємо
їх до вже викладеного (доскладаємо з них ціле). Що у нас вийшло? Як це записати
у вигляді дробу?
Зверніть
увагу на те, що зараз ми використовуємо як наочність піцу з різними шматочками.
Такого ще не було!
Чи
правильно це, адже частинки насправді різні? Зверніть увагу: частинки
однакового розміру і саме це для нас головне, адже запису дробів як і чисел
відповідає кількість (величина).
Отже,
формулюємо як потрібно додавати дроби: додаємо чисельник першого дробу до
чисельника другого — записуємо дріб: чисельник
— сума чисельників доданків, знаменник — незмінний. Чому ж чисельник
змінюється, а знаменник — ні? А тому що частини цілого ми не змінюємо — ми
змінюємо тільки їх кількість. Це повністю відповідає змісту арифметичної
операції додавання.
Ви
запитаєте, чому ж ми спочатку діяли з наочністю інтуїтивно виходячи із змісту
операції додавання і тільки зараз формулюємо правило. (Насправді додам, що ми
вже з першогоуроку вивчення дробів потроху готували дітей до цього кроку. Крок за кроком
ми пояснювали зміст роботи з дробами і діти все більше заглиблювалися в тему.) Не варто робити узагальнення раніше, ніж
діти зрозуміють зміст своїх дій. Тож все по черзі і так маленькими, але
впевненими кроками ми просуваємося до розуміння таємниць дробів.
Закладаємо міцний фундамент майбутнього
Звісно,
далеко не завжди ми будемо працювати з такою надто наочною наочністю. Варто
перейти до універсальнішої — зекономити собі час на виготовлення та зробити важливий
крок до узагальнення — перейти до абстрактніших дії, адже діти вже мають добре
розуміти зміст того, що роблять.
Такий
крок необхідний, адже діти не зможуть спиратися на наочність, коли будемо
працювати із знаменниками 25, 45, 100 тощо. Але вони мають добре уявляти зміст
своїх дій. Тож зараз ми закладаємо фундамент майбутнього, тому не поспішайте і
будуйте міцний фундамент.
У цей
час суперпомічником стане математичний планшет — саме з його допомогою ми і здійснімо цей крок — дії з дробами
будуть наочними і зрозумілими, але й абстрактнішими.
Спочатку,
коли вивчаємо додавання, діємо так: добираємо частини, кількість яких позначає
перший дріб (перший доданок). Потім докладаємо частини, кількість яких позначає
другий дріб (другий доданок). Що вийшло? Як написати дріб-суму?
Як можна
обчислити чисельник без наочності? Це запитання педагогам іноді хочеться задати
якомога раніше, адже здається, що все і вже зрозуміло. Але не поспішайте,
памʼятайте, що дроби складна тема і дітям треба звикнути рахувати не цілі
обʼєкти, а їх частини. Тож до відповіді на це запитання варто підводити дітей
обережно і поступово, задавати тоді, коли ви вже впевнені, що діти добре
зрозуміли зміст матеріалу і завдань, не втративши звʼязку зі змістом матеріалу.
Головне
для нас — бути певними, що діти не автоматично роблять певні математичні дії, а
можуть пояснити на наочних прикладах чому діють саме так. Інакше буде дуже
складно вивчати дії з дробами далі і переходити до дій з різними знаменниками.
Таким
чином ми здійснимо плавний необхідний нам перехід та підготуємо дітей до
наступного дослідження дробів.
Незвичні дроби: що вони означають
Досі
у дробах, які ми використовували, знаменник був більшим, ніж чисельник. Тобто
як ми бачили завдяки наочності такі
дроби позначають менше, ніж ціле. Зараз ускладнення — використовуємо дроби
з чисельником більшим, ніж знаменник. Їх ще називають неправильними дробами. Що це означає? Розмірковуємо разом з дітьми.
Діти
вибирають частинки, з яких можна скласти ціле — записують «1», решту частинок
записують дробом. А чи може у дробах ховатися тільки ціле? Звісно, може!
А ще
запропонуйте дітям вигадати приклади, результатом яких будуть такі дроби — 2
2/3, 4 1/5 тощо.
Як же
проілюструвати неправильні дроби? Не повірите, але і тут стане у пригоді математичний планшет, адже це універсальний посібник! Тільки цього разу треба взяти
два планшета — починаємо викладати суму на одному, склали ціле, перейшли до
другого і складаємо далі. Таким чином діти наочно бачать — ціле (1) та дріб і легко
записують результат додавання, наочно бачать чому він саме такий і розуміють як
перейти до обчислень без опори на наочність.
Завантажте презентацію «Смачні дроби. Частина 3. Додаємо дроби» для роботи з дітьми.
Раджу
вмикати режим перегляду розвʼязування завдань (кнопка «Розвʼязати» у
презентації) для закріплення, після того як діти вже виконали завдання. Звісно,
можна діяти інакше — розглядати з дітьми розвʼязування одного завдання, а потім
давати дітям можливість виконати подібні завдання вже самостійно. Але такий спосіб
я вважаю неефективним, адже діти можуть розпочати діяти за інструкцією, не
заглиблюючись у зміст своїх дій.
Зміцнюємо розуміння дробів, або практика — найкращий вчитель
Для закріплення
матеріалу дайте дітям різні завдання на дроби (вигадуйте будь-які завдання, а
не завдання на певну тему — наприклад тільки на порівняння дробів), адже тільки
так можна зрозуміти наскільки добре діти вивчили зміст теми.
А
краще нехай учні самостійно один одному вигадуватимуть завдання і одразу
розвʼязуватимуть їх. Так діти побачать наскільки різною по складності може бути
робота з дробами і можливо вигадають як цю складність можна подолати.
Одразу
скажу, що часто діти дійсно самі вигадують як діяти з дробами з різними
знаменниками, але при умові, що вони добре зрозуміли що таке дроби і вміють
користуватися наочністю.
Далі
будуть задачки-історії про дроби…
Ірина
СТЕЦЕНКО,
наукова співробітниця Міжнародного науково-навчального центру
інформаційних технологій та систем Національної академії наук України
та Міністерства освіти і науки України,
авторка технології «Логіки світу»
для дітей від 4 до 12 років
Читайте
роздуми щодо теми блогу


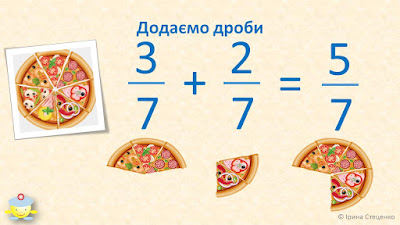







Немає коментарів:
Дописати коментар