Множини навколо нас: завдання з трьома колами (продовження)

Математика для дошкільнят та молодших школярів

Початок публікації читайте тут

Завдання 1

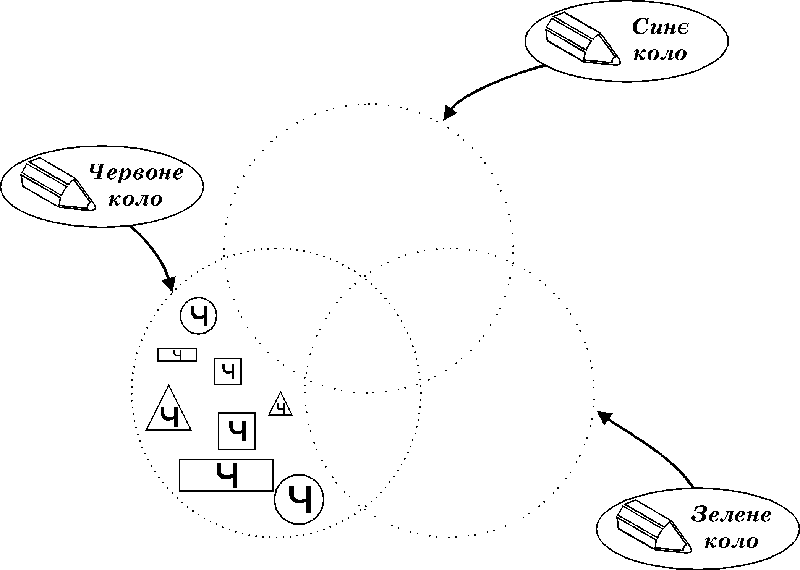
Розмісти геометричні фігури на сторінці так, щоб до середини червоного кола потрапили усі червоні фігури, до середини зеленого кола — всі трикутники, до середини синього кола — усі великі фігури.

Послідовно вибиратимемо геометричні фігури з набору і розташуватимемо їх на сторінці.

Знайдемо всі геометричні фігури, що потрапили до середини червоного кола. До середини червоного кола потрапили усі трикутники червоного кольору, усі квадрати червоного кольору, всі кола червоного кольору і всі прямокутники червоного кольору. Покладемо їх на сторінку в середину червоного кола.

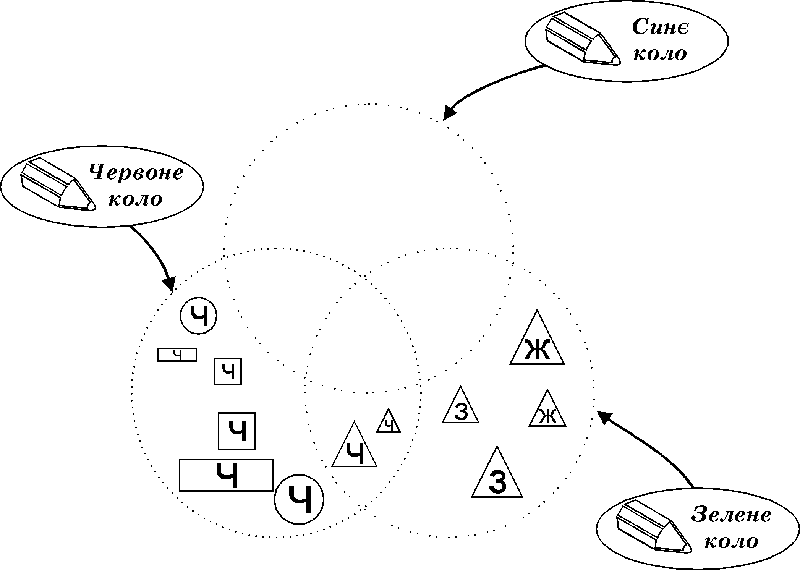
Які геометричні фігури потрапили до перетину червоного і зеленого кіл? У середині зеленого кола мають розміщуватися всі трикутники. Серед усіх геометричних фігур, розміщених в середині червоного кола, виберемо усі трикутники і покладемо їх до перетину червоного і зеленого кіл. Великі і маленькі трикутники червоного кольору потрапили до перетину цих кіл.

Які геометричні фігури ще не розміщені в середині зеленого кола? (Розглядаємо всі геометричні фігури, які ще не потрапили до середини жодного кола.) В середину зеленого кола ще потрібно покласти великі і маленькі трикутники жовтого і зеленого кольорів. Будьте уважними! Ці трикутники не повинні потрапити до перетину кіл.

Які геометричні фігури потрапили до середини синього кола? До середини синього кола потрапили великі квадрати зеленого і жовтого кольорів, великі кола зеленого і жовтого кольору, великі прямокутники зеленого і жовтого кольорів.

Знайдемо перетин червоного і синього кіл. Подивимося, які геометричні фігури, що зараз розмістилися у середині червоного кола, можуть розміститися і в середині синього кола. Ці фігури і потраплять до перетину кіл. До перетину червоного і синього кіл потрапили такі геометричні фігури червоного кольору: великі прямокутники, великі квадрати і великі кола. Які ще геометричні фігури на малюнку можуть розміститися у середині синього кола? Звісно, такі фігури треба шукати в перетині червоного і зеленого кіл. Великий червоний трикутник теж може розміститися у перетині синього і червоного кіл, але він має також належати до перетину зеленого і червоного кіл. Тому великий червоний трикутник нам слід розмістити в перетині одразу трьох кіл.

До перетину зеленого і синього кіл потрапили великі трикутники зеленого і жовтого кольорів.

Таким чином, до перетину червоного і синього кіл потрапили всі великі геометричні фігури червоного кольору, до перетину синього і зеленого кіл потрапили всі великі трикутники, до перетину червоного і зеленого кіл — усі червоні трикутники. Великі червоні трикутники потрапили до перетину усіх кіл.

Завдання 2

Розмісти геометричні фігури на сторінці так, щоб до середини червоного кола потрапили всі круги, до середини зеленого кола — усі квадрати, а до середини синього кола — всі червоні фігури.

Поясни, чому деякі області залишилися порожніми.

Виберемо з набору великі і маленькі круги, розмістимо їх у середині червоного кола, але зовні усіх інших кіл. У середину зеленого кола помістимо всі квадрати, але всі вони спочатку розміщуватимемо зовні синього і червоного кіл.

Які геометричні фігури належатимуть до перетину зеленого і червоного кіл? Перетин цих кіл буде порожнім, тому що серед кіл і квадратів немає спільних геометричних фігур (немає геометричних фігур, які можна розмістити в середині і зеленого, і червоного кіл). Геометричні фігури не можуть водночас бути круглими (без кутів) і квадратами (з кутами).

Які геометричні фігури ми розмістимо у середині синього кола? У середині синього кола ми розмістимо всі геометричні фігури червоного кольору, що лишилися в нашому наборі.

Які геометричні фігури належать до перетину червоного і синього кіл? До перетину червоного і синього кіл належатимуть усі круги червоного кольору, тому що до середини синього кола потрапили геометричні фігури червоного кольору, а до середини червоного кола потрапили всі круги. Прямокутники і трикутники мають кути і тому не можуть потрапити до середини червоного кола. Тому прямокутники і трикутники не можуть належати до перетину червоного і синього кіл.

До перетину зеленого і синього кіл потрапили всі квадрати червоного кольору.

Неважко помітити, що жодна геометрична фігура не належить до перетину усіх трьох кіл. Чому? Тому що жодна геометрична фігура не потрапила до перетину червоного і зеленого кіл, а частина цього перетину належить і перетину всіх трьох кіл.

Таким чином, жоден елемент не потрапить до перетину всіх трьох кіл, якщо хоча один перетин будь-яких двох кіл порожній. Цей висновок можна підтвердити, розв’язуючи інші завдання з використанням трьох кіл.

Під час розв’язування кожного завдання намагайтесь разом з малюками знайти щось цікаве, що відрізняє це завдання від інших такого типу. Вкрай важливо, щоб розв’язуючи різні завдання кожна дитина помітила щось нове, зробила для себе маленьке відкриття.

Відтак з трьома колами можна розв’язувати такі самі завдання, як і з одним та з двома колами.

Ірина СТЕЦЕНКО,

науковий співробітник Міжнародного науково-навчального центру інформаційних технологій та систем Національної академії наук України

та Міністерства освіти і науки України,

автор технології «Логіки світу»

для дітей від 4 до 12 років

Дізнайтеся про що блог

Читайте роздуми щодо теми блогу

Автор: Ірина Стеценко